A stone thrown vertically upwards ……… = To prove that the time taken to reach the maximum height (going up) is equal to the time taken to return to the starting point (coming down) for a stone thrown vertically upwards, we can use some basic kinematic equations.
Let’s consider the motion of the stone.
- On the way up:
Initial velocity, ( u ) (upward)
Final velocity at the top, ( v = 0 ) (at maximum height)
Distance covered, ( h ) (maximum height reached)
Acceleration, ( g ) (acceleration due to gravity)
The equation for the maximum height reached can be given by:
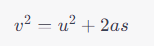
At the topmost point, ( v = 0 ):
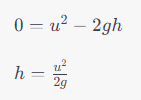
- On the way down:
The initial velocity is 0 when the stone reaches the highest point and starts falling back.
The distance is still ( h ) (the stone needs to cover the same distance to get back to the starting point).
Acceleration, ( g ) (downward this time)
Using the equation of motion:
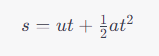
For the downward journey, initial velocity is 0:
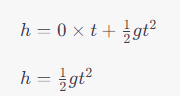
Now, let’s solve for time, ( t ), in terms of ( h ):
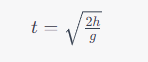
We found earlier that
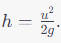
. Substituting this value of ( h ) in the time equation:

Now, the time taken to go up (to reach the maximum height) was
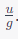
and interestingly, the time taken to come down is also
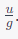
Thus, the time taken to go up is the same as the time taken to come down.